, page 6

11 Basic functions of a complex variable

Let us recall the definition of a complex exponent – ​​. Then

Maclaurin series expansion. The radius of convergence of this series is +∞, which means that the complex exponential is analytic on the entire complex plane and

(exp z)"=exp z; exp 0=1. (2)

The first equality here follows, for example, from the theorem on term-by-term differentiation of a power series.

11.1 Trigonometric and hyperbolic functions

Sine of a complex variable called function

Cosine of a complex variable there is a function

Hyperbolic sine of a complex variable is defined like this:

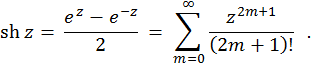
Hyperbolic cosine of a complex variable-- this is a function

Let us note some properties of the newly introduced functions.

A. If x∈ ℝ, then cos x, sin x, cosh x, sh x∈ ℝ.

B. The following connection exists between trigonometric and hyperbolic functions:

cos iz=ch z; sin iz=ish z, ch iz=cos z; sh iz=isin z.

B. Basic trigonometric and hyperbolic identities:

cos 2 z+sin 2 z=1; ch 2 z-sh 2 z=1.

Proof of the main hyperbolic identity.

The main trigonometric identity follows from the main hyperbolic identity when taking into account the connection between trigonometric and hyperbolic functions (see property B)

G Addition formulas:

In particular,

D. To calculate derivatives of trigonometric and hyperbolic functions, one should apply the theorem on term-by-term differentiation of power series. We get:

(cos z)"=-sin z; (sin z)"=cos z; (ch z)"=sh z; (sh z)"=ch z.

E. The functions cos z, ch z are even, and the functions sin z, sin z are odd.

J. (Frequency) The function e z is periodic with period 2π i. The functions cos z, sin z are periodic with a period of 2π, and the functions ch z, sin z are periodic with a period of 2πi. Moreover,

Applying the sum formulas, we get

Z. Expansion into real and imaginary parts:

If a single-valued analytic function f(z) bijectively maps a domain D onto a domain G, then D is called a univalence domain.

AND. Region D k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

Proof. From relation (5) it follows that the mapping exp:D k → ℂ is injective. Let w be any non-zero complex number. Then, solving the equations e x =|w| and e iy =w/|w| with real variables x and y (y is chosen from a half-interval for n > 1 is different from zero at all points except z = 0. Writing w and z in exponential form in formula (4), we obtain that From formula (5) it is clear that complex numbers Z\ and z2 such that where k is an integer, go to one point w. This means that for n > 1 the mapping (4) is not univalent on the plane z. The simplest example of a domain in which the mapping ω = zn is univalent. sector where a is any real number. In domain (7), mapping (4) is conformally multivalued, since for each complex number z = ε1в Ф 0 one can specify n different complex numbers such that their nth degree is equal to z: Note that a polynomial of degree n of a complex variable z is a function where are given complex numbers, and ao Φ 0. A polynomial of any degree is an analytic function on the entire complex plane. 2.3. Fractional-rational function A fractional-rational function is called a function of the form where) are polynomials of the complex variable z. The fractional rational function is analytic throughout the plane, except for those points at which the denominator Q(z) vanishes. Example 3. The Zhukovsky function__ is analytic in the entire plane r, excluding the point r = 0. Let us find out the conditions for the region of the complex plane under which the Zhukovsky function considered in this region will be univalent. M Let the points Z) and zj be transferred by function (8) to one point. Then at we get that So, for the Zhukovsky function to be univalent, it is necessary and sufficient to satisfy the condition An example of a region that satisfies the univalence condition (9) is the exterior of the circle |z| > 1. Since the derivative of the Zhukovsky function Elementary functions of a complex variable Fractional-rational functions Power function Exponential function Logarithmic function Trigonometric and hyperbolic functions is nonzero everywhere except at points, the mapping of the domain carried out by this function will be conformal (Fig. 13). Note that the interior of the unit disk |I is also the domain of univalence of the Zhukovsky function. Rice. 13 2.4. Exponential function We define the exponential function ez for any complex number z = x + y by the following relation: For x = 0 we obtain Euler’s formula: Let us describe the main properties of the exponential function: 1. For real z this definition coincides with the usual one. This can be verified directly by setting y = 0 in formula (10). 2. The function ez is analytic on the entire complex plane, and for it the usual differentiation formula is preserved. 3. For the function ez the addition theorem is preserved. Let us assume 4. The function ez is periodic with an imaginary main period 2xi. In fact, for any integer k On the other hand, if then from definition (10) it follows that Whence it follows that, or where n is an integer. The strip does not contain a single pair of points connected by relation (12), therefore, from the study carried out it follows that the mapping w = e" is single in the strip (Fig. 14). Since it is a derivative, this mapping is conformal. Note niv. Function g.g is univalent in any strip 2.5. Logarithmic function From the equation where the unknown is given, we obtain Hence, the inverse function of the function is defined for any and is represented by the formula where This multi-valued function is called logarithmic and is denoted as follows The value arg z is called the principal value of the logarithm and denoted by Then for Ln z we obtain formula 2.6. Trigonometric and hyperbolic functions From Euler’s formula (11) for real y we obtain From where we define the trigonometric functions sin z and cos z for any complex number z using the following formulas: The sine and cosine of a complex argument have interesting properties Let us list the main ones: The functions sinz and cos z: 1) for real z -x coincide with ordinary sines and cosines; 2) analytic on the entire complex plane; 3) obey the usual differentiation formulas: 4) are periodic with a period of 2π; 5) sin z is an odd function, and cos z is an even function; 6) the usual trigonometric relations are preserved. All of the listed properties can be easily obtained from formulas (15). The functions tgz and ctgz in the complex domain are determined by the formulas, and hyperbolic functions - by the formulas "Hyperbolic functions are closely related to trigonometric functions. This relationship is expressed by the following equalities: The sine and cosine of a complex argument have another important property: on the complex plane |\ take arbitrarily large positive values. Let's show this. Using properties 6 and formulas (18), we obtain that Elementary functions of a complex variable Fractional rational functions Power function Exponential function Logarithmic function Trigonometric and hyperbolic functions From where, Assuming, we have Example 4. It is easy to check that -4 In fact ,

Functions of a complex variable.
Differentiation of functions of a complex variable.

This article opens a series of lessons in which I will consider typical problems related to the theory of functions of a complex variable. To successfully master the examples, you must have basic knowledge of complex numbers. In order to consolidate and repeat the material, just visit the page. You will also need the skills to find second order partial derivatives. Here they are, these partial derivatives... even now I was a little surprised how often they occur...

The topic that we are beginning to examine does not present any particular difficulties, and in the functions of a complex variable, in principle, everything is clear and accessible. The main thing is to adhere to the basic rule, which I derived experimentally. Read on!

Concept of a function of a complex variable

First, let's refresh our knowledge about the school function of one variable:

Single variable function is a rule according to which each value of the independent variable (from the domain of definition) corresponds to one and only one value of the function. Naturally, “x” and “y” are real numbers.

In the complex case, the functional dependence is specified similarly:

Single-valued function of a complex variable- this is the rule according to which everyone comprehensive the value of the independent variable (from the domain of definition) corresponds to one and only one comprehensive function value. The theory also considers multi-valued and some other types of functions, but for simplicity I will focus on one definition.

What is the difference between a complex variable function?

The main difference: complex numbers. I'm not being ironic. Such questions often leave people in a stupor; at the end of the article I’ll tell you a funny story. In class Complex numbers for dummies we considered a complex number in the form . Since now the letter “z” has become variable, then we will denote it as follows: , while “x” and “y” can take different valid meanings. Roughly speaking, the function of a complex variable depends on the variables and , which take on “ordinary” values. The following point logically follows from this fact:

The function of a complex variable can be written as:
, where and are two functions of two valid variables.

The function is called real part functions
The function is called imaginary part functions

That is, the function of a complex variable depends on two real functions and . To finally clarify everything, let’s look at practical examples:

Example 1

Solution: The independent variable “zet”, as you remember, is written in the form , therefore:

(1) We substituted .

(2) For the first term, the abbreviated multiplication formula was used. In the term, the parentheses have been opened.

(3) Carefully squared, not forgetting that

(4) Rearrangement of terms: first we rewrite the terms , in which there is no imaginary unit(first group), then the terms where there are (second group). It should be noted that shuffling the terms is not necessary, and this step can be skipped (by actually doing it orally).

(5) For the second group we take it out of brackets.

As a result, our function turned out to be represented in the form

Answer:
– real part of the function.
– imaginary part of the function.

What kind of functions did these turn out to be? The most common functions of two variables from which you can find such popular partial derivatives. Without mercy, we will find it. But a little later.

Briefly, the algorithm for the solved problem can be written as follows: we substitute , into the original function, carry out simplifications and divide all terms into two groups - without an imaginary unit (real part) and with an imaginary unit (imaginary part).

Example 2

Find the real and imaginary part of the function

This is an example for you to solve on your own. Before you rush into battle on the complex plane with your checkers drawn, let me give you the most important advice on the topic:

BE CAREFUL! You need to be careful, of course, everywhere, but in complex numbers you should be more careful than ever! Remember that, carefully open the brackets, do not lose anything. According to my observations, the most common mistake is the loss of a sign. Don't rush!

Full solution and answer at the end of the lesson.

Now the cube. Using the abbreviated multiplication formula, we derive:
.

Formulas are very convenient to use in practice, since they significantly speed up the solution process.

Differentiation of functions of a complex variable.

I have two news: good and bad. I'll start with the good one. For a function of a complex variable, the rules of differentiation and the table of derivatives of elementary functions are valid. Thus, the derivative is taken in exactly the same way as in the case of a function of a real variable.

The bad news is that for many complex variable functions there is no derivative at all, and you have to figure out is it differentiable one function or another. And “figuring out” how your heart feels is associated with additional problems.

Let's consider the function of a complex variable. In order to this function was differentiable necessary and sufficient:

1) So that first-order partial derivatives exist. Forget about these notations right away, since in the theory of functions of a complex variable a different notation is traditionally used: .

2) To carry out the so-called Cauchy-Riemann conditions:

Only in this case will the derivative exist!

Example 3

Solution is divided into three successive stages:

1) Let's find the real and imaginary parts of the function. This task was discussed in previous examples, so I’ll write it down without comment:

Since then:

Thus:

– imaginary part of the function.

Let me touch on one more technical point: in what order write the terms in the real and imaginary parts? Yes, in principle, it doesn’t matter. For example, the real part can be written like this: , and the imaginary one – like this: .

2) Let us check the fulfillment of the Cauchy-Riemann conditions. There are two of them.

Let's start by checking the condition. We find partial derivatives:

Thus, the condition is satisfied.

Of course, the good news is that partial derivatives are almost always very simple.

We check the fulfillment of the second condition:

The result is the same, but with opposite signs, that is, the condition is also fulfilled.

The Cauchy-Riemann conditions are satisfied, therefore the function is differentiable.

3) Let's find the derivative of the function. The derivative is also very simple and is found according to the usual rules:

The imaginary unit is considered a constant during differentiation.

Answer: – real part, – imaginary part.
The Cauchy-Riemann conditions are satisfied, .

There are two more ways to find the derivative, they are, of course, used less frequently, but the information will be useful for understanding the second lesson - How to find a function of a complex variable?

The derivative can be found using the formula:

In this case:

Thus

We have to solve the inverse problem - in the resulting expression we need to isolate . In order to do this, it is necessary in the terms and outside the brackets:

The reverse action, as many have noticed, is somewhat more difficult to perform; to check, it is always better to take the expression on a draft or orally open the parentheses back, making sure that the result is exactly

Mirror formula for finding the derivative:

In this case: , That's why:

Example 4

Determine the real and imaginary parts of a function . Check the fulfillment of the Cauchy-Riemann conditions. If the Cauchy-Riemann conditions are met, find the derivative of the function.

A short solution and an approximate sample of the final design at the end of the lesson.

Are the Cauchy-Riemann conditions always satisfied? Theoretically, they are not fulfilled more often than they are fulfilled. But in practical examples I don’t remember a case where they were not fulfilled =) Thus, if your partial derivatives “do not converge,” then with a very high probability you can say that you made a mistake somewhere.

Let's complicate our functions:

Example 5

Determine the real and imaginary parts of a function . Check the fulfillment of the Cauchy-Riemann conditions. Calculate

Solution: The solution algorithm is completely preserved, but at the end a new point will be added: finding the derivative at a point. For the cube, the required formula has already been derived:

Let's define the real and imaginary parts of this function:

Attention and attention again!

Since then:


Thus:
– real part of the function;
– imaginary part of the function.

Checking the second condition:

The result is the same, but with opposite signs, that is, the condition is also fulfilled.

The Cauchy-Riemann conditions are satisfied, therefore the function is differentiable:

Let's calculate the value of the derivative at the required point:

Answer:, , the Cauchy-Riemann conditions are satisfied,

Functions with cubes are common, so here’s an example to reinforce:

Example 6

Determine the real and imaginary parts of a function . Check the fulfillment of the Cauchy-Riemann conditions. Calculate.

Solution and example of finishing at the end of the lesson.

In the theory of complex analysis, other functions of a complex argument are also defined: exponent, sine, cosine, etc. These functions have unusual and even bizarre properties - and this is really interesting! I really want to tell you, but here, as it happens, is not a reference book or textbook, but a solution book, so I will consider the same problem with some common functions.

First about the so-called Euler's formulas:

For anyone valid numbers, the following formulas are valid:

You can also copy it into your notebook as reference material.

Strictly speaking, there is only one formula, but for convenience they usually write special case with a minus in the indicator. The parameter does not have to be a single letter; it can be a complex expression or function, it is only important that they accept only valid meanings. Actually, we will see this right now:

Example 7

Find the derivative.

Solution: The general line of the party remains unshakable - it is necessary to distinguish the real and imaginary parts of the function. I will give a detailed solution and comment on each step below:

Since then:

(1) Substitute “z” instead.

(2) After substitution, you need to select the real and imaginary parts first in the indicator exhibitors. To do this, open the brackets.

(3) We group the imaginary part of the indicator, placing the imaginary unit out of brackets.

(4) We use the school action with degrees.

(5) For the multiplier we use Euler’s formula, and .

(6) Open the brackets, resulting in:

– real part of the function;
– imaginary part of the function.

Further actions are standard; let’s check the fulfillment of the Cauchy-Riemann conditions:

Example 9

Determine the real and imaginary parts of a function . Check the fulfillment of the Cauchy-Riemann conditions. So be it, we won’t find the derivative.

Solution: The solution algorithm is very similar to the previous two examples, but there are very important points, so I will again comment on the initial stage step by step:

Since then:

1) Substitute “z” instead.

(2) First, we select the real and imaginary parts inside the sinus. For these purposes, we open the brackets.

(3) We use the formula, and .

(4) Use parity of hyperbolic cosine: And oddity of hyperbolic sine: . Hyperbolics, although out of this world, are in many ways reminiscent of similar trigonometric functions.

As a result:
– real part of the function;
– imaginary part of the function.

Attention! The minus sign refers to the imaginary part, and under no circumstances should we lose it! For a clear illustration, the result obtained above can be rewritten as follows:

Let's check the fulfillment of the Cauchy-Riemann conditions:

The Cauchy-Riemann conditions are satisfied.

Answer:, , the Cauchy-Riemann conditions are satisfied.

Ladies and gentlemen, let’s figure it out on our own:

Example 10

Determine the real and imaginary parts of the function. Check the fulfillment of the Cauchy-Riemann conditions.

I deliberately chose more difficult examples, because everyone seems to be able to cope with something, like shelled peanuts. At the same time, you will train your attention! Nut cracker at the end of the lesson.

Well, in conclusion, I’ll look at another interesting example when a complex argument is in the denominator. It’s happened a couple of times in practice, let’s look at something simple. Eh, I'm getting old...

Example 11

Determine the real and imaginary parts of the function. Check the fulfillment of the Cauchy-Riemann conditions.

Solution: Again it is necessary to distinguish the real and imaginary parts of the function.
If , then

The question arises, what to do when “Z” is in the denominator?

Everything is simple - the standard one will help method of multiplying the numerator and denominator by the conjugate expression, it has already been used in the examples of the lesson Complex numbers for dummies. Let's remember the school formula. We already have in the denominator, which means the conjugate expression will be . Thus, you need to multiply the numerator and denominator by: